Implementing Depth-First Search (DFS) Algorithm in Python: A Comprehensive Guide

Algorithm

1. Create a function called DFS with a starting vertex as the parameter.

2. Initialize an empty stack and an empty set to keep track of visited vertices.

3. Push the starting vertex onto the stack.

4. While the stack is not empty, do the following: a. Pop a vertex from the stack. b. If the vertex has not been visited, mark it as visited and process it. c. Push all the unvisited neighbors of the current vertex onto the stack.

5. Repeat steps 4 until the stack is empty.

Pseudo Code

function DFS(start_vertex):
    stack = empty stack
    visited = empty set
    push start_vertex onto stack

    while stack is not empty:
        current_vertex = pop from stack
        if current_vertex is not visited:
            mark current_vertex as visited
            process current_vertex
            push unvisited neighbors of current_vertex onto stack

Code

def DFS(start_vertex):
    stack = []
    visited = set()
    stack.append(start_vertex)

    while stack:
        current_vertex = stack.pop()
        if current_vertex not in visited:
            visited.add(current_vertex)
            process_vertex(current_vertex)
            stack.extend(neighbor for neighbor in get_neighbors(current_vertex) if neighbor not in visited)

Explanation

The depth-first search (DFS) algorithm starts from a given vertex and explores as far as possible along each branch before backtracking. It uses a stack data structure to keep track of vertices to visit. The algorithm begins by pushing the starting vertex onto the stack and continues until all vertices have been visited.

In the code, the DFS function takes a starting vertex as input. It initializes an empty stack and an empty set to track visited vertices. The starting vertex is pushed onto the stack. The algorithm then enters a loop where it pops a vertex from the stack, checks if it has been visited, marks it as visited, processes it, and pushes its unvisited neighbors onto the stack. This process continues until the stack is empty.

The process_vertex function represents the action to be performed on each visited vertex, and the get_neighbors function returns a list of neighbors for a given vertex.

Example

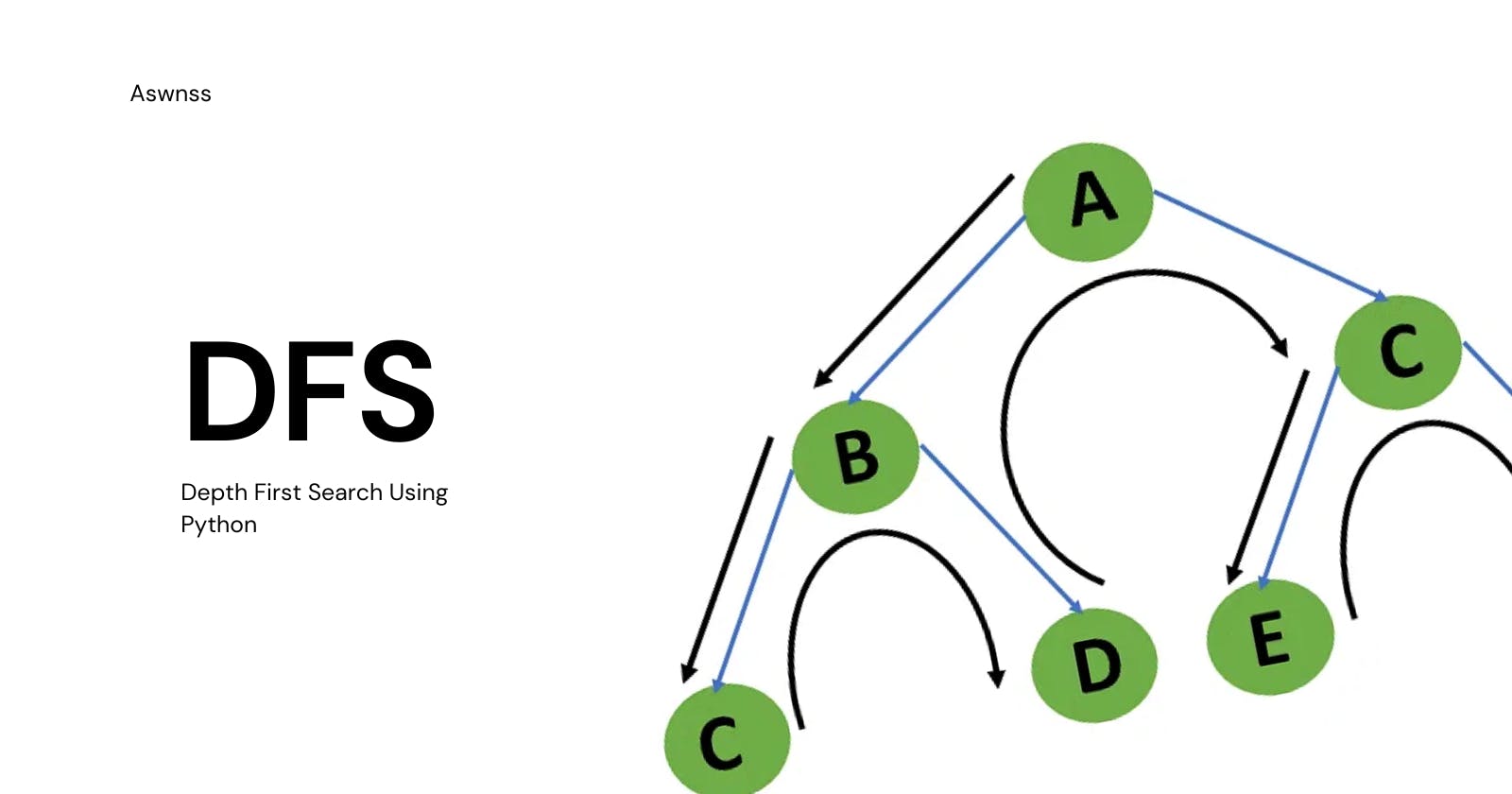
Consider a graph representing a social network where vertices represent users and edges represent connections between users. We want to perform a depth-first search starting from a specific user to find all the connected users.

pythonCopy code# Graph representation (adjacency list)
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# Function to process a visited vertex
def process_vertex(vertex):
    print(vertex)

# Function to get neighbors of a vertex
def get_neighbors(vertex):
    return graph[vertex]

# Perform DFS starting from vertex 'A'
DFS('A')

Output:

mathematicaCopy codeA
B
D
E
F
C

In this example, we start the DFS traversal from vertex 'A'. The algorithm visits each connected vertex in a depth-first manner, printing the vertex value. The traversal order is 'A' -> 'B' -> 'D' -> 'E' -> 'F' -> 'C'.

Extra

• You can modify the process_vertex function to perform any specific operations or calculations on the visited vertices.

• Ensure that the graph is represented appropriately in your code, either as an adjacency list or an adjacency matrix, depending on your specific implementation requirements.

• DFS is a recursive algorithm by nature, but it can also be implemented iteratively using a stack, as shown in the provided code.

• Experiment with different graph structures and visualize the DFS traversal to gain a better understanding of the algorithm.

By implementing the Depth-First Search algorithm in Python, you can explore and traverse graphs effectively, opening up possibilities for various graph-related problems and applications.

If you have any questions or need further clarification, please let me know. Happy coding with Depth-First Search!